2. String Rewriting Systems

Definitions of string rewriting systems.

A string rewriting system, also known as an abstract reduction system or abstract rewriting system, is a pair consisting of an alphabet A and a set of rewriting rules R, where R is a relation

\(\mathcal{R}\subseteq A^*\times A^*.\)

Here, A* denotes the free monoid generated by A, or the set of all strings over A equipped with concatenation of strings as its multiplication. It is not hard to see that concatenation is associative and the identity element is the empty word consisting of no letters, often denoted as

\(\varepsilon\)

or ““ for Python purposes. Note that rewriting rules are ordered pairs, meaning any rewriting happens in a specific order. We always assume that a word may rewrite to itself with precisely 0 applications of any rewriting rule.

Any string rewriting system defines a monoid presentation (or semigroup presentation, but we will focus on monoids) via the congruence closure of its set of rewriting rules. This provides a way to think about equivalence of words under the congruence as rewriting. Here, if two strings in A* are equal, such as a=b, then for any x and y in A* we have that xay=xby (by definition of congruence). We can say that xay rewrites to xby, denoted xay → xby or vice versa.

Now, let’s say that we have a monoid presentation and we would like to determine if two words are equal under the given presentation (or solve the word problem for that monoid). We could give a computer our presentation and tell it to determine if those words are equal by rewriting one into the other with the relations in the presentation like so: xaybz → xbybz → xbyaz (letting us conclude that xaybz=xbyaz). However, we will inevitably run into problems. For one, equalities in the presentation to not prescribe a direction for us to rewrite. Also, there are infinitely many ways that the rewritings could happen, or none at all (yet infinitely many ways we must rule out).

We then must make some specifications for the rewriting rules defined by a presentation. The following definition will be our most important.

Definition: A rewriting system (A,R) is Noetherian if there does not exist any infinite sequence of words in A* such that

\(x_1\rightarrow x_2\rightarrow x_3\rightarrow\cdots\text{ (for }x_i\in A^*,\text{ }i\in\mathbb{Z^+)}\)

and

\(\forall i\in\mathbb{Z}^+,\text{ }x_i\neq x_{i+1}.\)

That is, every rewriting of a word must terminate at some point. Any finite rewriting system (meaning one with a finite alphabet and finite set of rewriting rules) is Noetherian if it contains no “loops“, where there exist words x and y such that x→y and y→x using the rewriting rules in the system.

Definition: A word which does not contain as a subword the left hand side of any rewriting rule is called irreducible. That is, it cannot be written by the given rewriting system. If x and y are two words such that x→y and y is irreducible, then we say that y is a normal form for x.

Using just this definition a congruence class may contain several normal forms, or none at all! Luckily, we have the following theorems.

Theorem: Every word (and thus congruence class) has a normal form under a Noetherian rewriting system.

Proof: Let x be a word in A* and consider a sequence of rewritings of x which results in a word y. Since x has no normal form, y cannot be irreducible. Then y may be further rewritten, and hence x may be rewritten ad infinitum, so there exists an infinite sequence of rewritings of x (where each resulting word is not equal to the last). This contradicts the assumption that the rewriting system is Noetherian. □

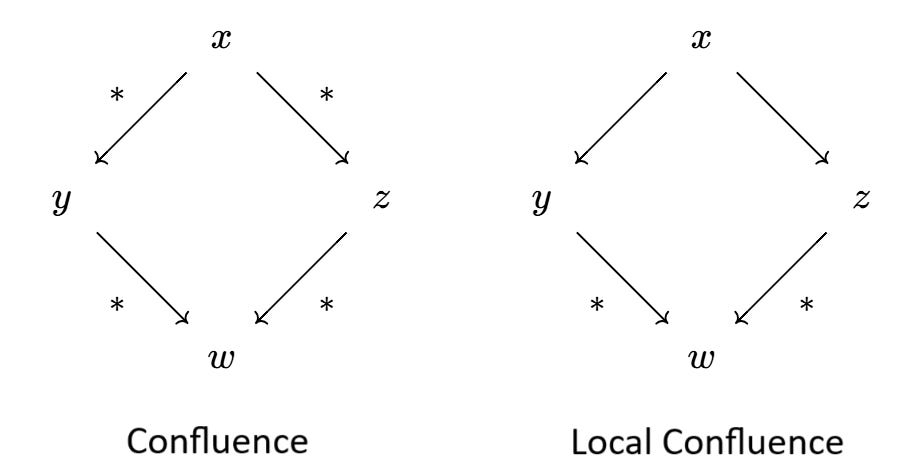
Definition: A rewriting system is confluent if for any word x in A*, if x rewrites to two words y and z, then there exists some word w such that y and z both rewrite to w. A rewriting system is locally confluent if for any x in A*, if x rewrites to both y and z with just one application of any rewriting rule, then y and z both rewrite to some w in A*.

In the below diagram, I depict confluence and local confluence. Arrows with stars represent rewritings that may use zero or multiple rules, whereas arrows with no stars use precisely one rewriting rule. This notation is typical, but I neglect it in this series.

Theorem: A Noetherian rewriting system is confluent iff it is locally confluent.

I do not give the proof of the theorem, but it should be accessible to the reader and can be found in Book & Otto (1993).